第三节 双向板肋梁楼盖设计
2.3.1 双向板肋梁楼盖按弹性理论计算结构内力
1、单块矩形双向板(单区格双向板)
按弹性理论取微元体,建立微分方程式并求解,根据边界条件可以求出板的内力与变形。或纵横各取一单元宽板带,按交点处挠度相等进行荷载分配。
单块矩形双向板按弹性薄板小挠度理论计算是相当复杂的,为了实用方便,根据板四周的支承情况和板两个方向跨度的比值,将按弹性理论的计算结果制成数字表格,供设计时查用。
单位板宽内弯矩和挠度计算方法:
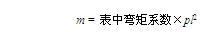
2、多跨连续双向板(多区格双向板)
(1)板跨中最大正弯矩计算(活荷载棋盘式布置)
分为两种荷载情况:满布同向荷载和满布反向荷载。
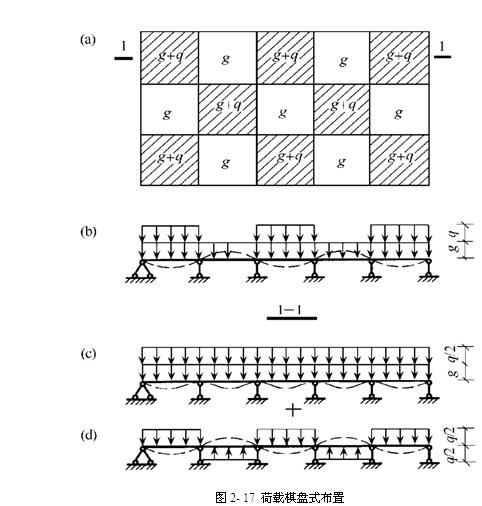
(2)支座处板最大负弯矩计算(活荷载近似按满布)
近似将恒载及活荷载作用在所有区格板上,则各内部区格板均按四边固定板计算支座弯矩。
3、双向板楼盖支承梁内力计算
由每区格四角按45°对角线将区格划分为四块,这样所形成的图形是三角形和梯形。按照此形状每块上的恒载和活载传递给相邻的支承梁。不考虑板的连续性。
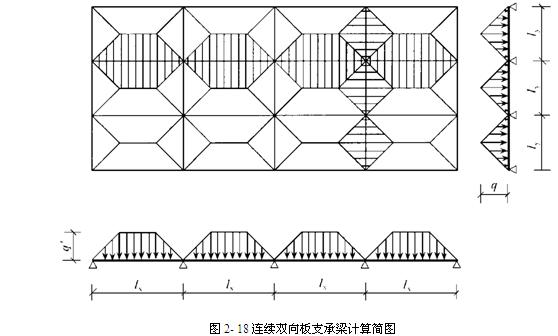
2.3.2 钢筋混凝土双向板极限承载力分析
1、双向板肋梁楼盖受力特点
四边简支双向板在均布荷载作用下的试验研究大致经过以下四个阶段:弹性、开裂、与裂缝相交的钢筋屈服、形成机构。
长跨方向的最大弯矩并不发生在跨中截面,二是在离板边1/2短跨跨长处,板传给四边支座的压力沿边长不是均匀分布的,而是中部大、两端小。
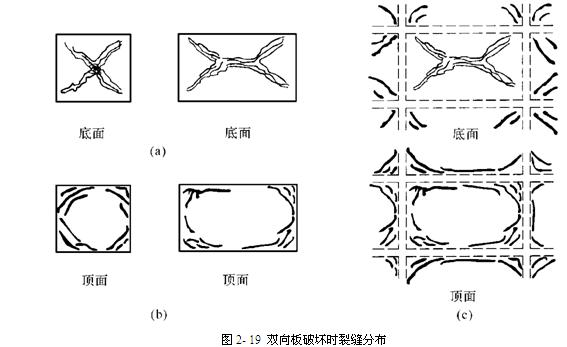
2、塑性铰线及其确定
板中连续的一些截面均出现塑性铰,连在一起称为塑性铰线。
板的极限荷载:当板中出现足够数量的塑性铰线后,板成为机动体系,达到其承载能力极限状态而破坏,这时板所承受的荷载为板的极限荷载。
板中塑性铰线的分布形式与以下因素有关:
(1) 板的平面形状
(2) 周边支承条件
(3) 两方向跨中、支座的配筋量
(4) 荷载类型等
3、结构极限承载力分析的基本原理
钢筋混凝土双向板具有一定的塑性性质和塑性变形能力,采用塑性理论进行计算与实际较符合,且可节省钢筋。
双向板为高次超静定结构,按塑性理论求精确解很困难,只能求得上限解和下限解。常用方法有极限平衡法和能量法。
现以极限平衡法为例,进行推导
基本假定
(1) 在最大弯矩处形成塑性铰线
(2) 塑性铰线为直线
(3) 板块视为刚性平面
(4) 最危险塑性铰线,最小极限荷载
(5) 塑性铰线上只作用常量弯矩
计算方法
在实际工程设计中,对于承受均布荷载的矩形板,板的正塑性铰线可采用一种固定的分布形式,即板角部的斜向塑性铰线与板夹角取45°。
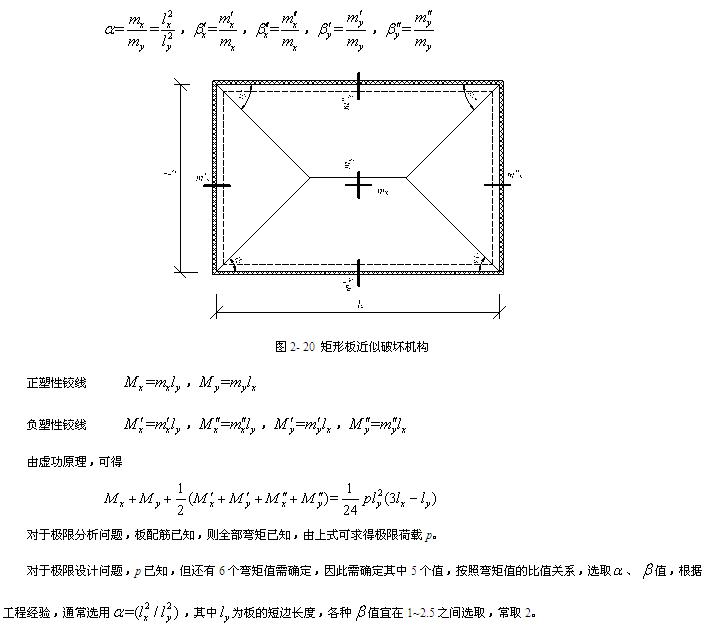
2.3.3 双向板肋梁楼盖按塑性理论计算步骤
双向板肋梁楼盖通常是多跨连续,亦即楼盖由一些双向板区格组成。对于内部双向板区格按四边固定单块板计算,边区格及角区格按实际支承情况的单块板计算。掌握了单块双向板的计算方法,也就能计算多跨双向板楼盖。
计算步骤
(1)将楼盖划分为不同的双向板曲格。

2、板的配筋构造
双向板的受力钢筋沿板区格平面纵横两个方向配置,配筋方式有弯起式和分离式两种,与单向板中的配筋方式类似。
(1)按弹性理论计算时:正弯矩钢筋(中间板带,边板带)
负弯矩钢筋(沿支座均匀配置)
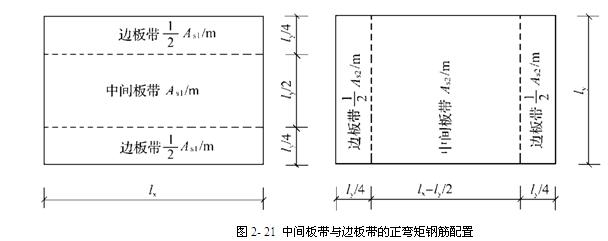
(2)按塑性理论计算时:配筋应符合内力计算的假定,跨内正弯矩钢筋可沿全板均匀配置,支座上的负弯矩钢筋按计算值沿支座均匀配置。
双向板受力钢筋的直径、间距和弯起点、切断点的位置,以及沿墙边、墙角处的构造钢筋,均与单向板肋梁楼盖的有关规定相同。
1、单块矩形双向板(单区格双向板)
按弹性理论取微元体,建立微分方程式并求解,根据边界条件可以求出板的内力与变形。或纵横各取一单元宽板带,按交点处挠度相等进行荷载分配。
单块矩形双向板按弹性薄板小挠度理论计算是相当复杂的,为了实用方便,根据板四周的支承情况和板两个方向跨度的比值,将按弹性理论的计算结果制成数字表格,供设计时查用。
单位板宽内弯矩和挠度计算方法:
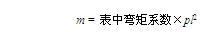
2、多跨连续双向板(多区格双向板)
(1)板跨中最大正弯矩计算(活荷载棋盘式布置)
分为两种荷载情况:满布同向荷载和满布反向荷载。

(2)支座处板最大负弯矩计算(活荷载近似按满布)
近似将恒载及活荷载作用在所有区格板上,则各内部区格板均按四边固定板计算支座弯矩。
3、双向板楼盖支承梁内力计算
由每区格四角按45°对角线将区格划分为四块,这样所形成的图形是三角形和梯形。按照此形状每块上的恒载和活载传递给相邻的支承梁。不考虑板的连续性。

2.3.2 钢筋混凝土双向板极限承载力分析
1、双向板肋梁楼盖受力特点
四边简支双向板在均布荷载作用下的试验研究大致经过以下四个阶段:弹性、开裂、与裂缝相交的钢筋屈服、形成机构。
长跨方向的最大弯矩并不发生在跨中截面,二是在离板边1/2短跨跨长处,板传给四边支座的压力沿边长不是均匀分布的,而是中部大、两端小。

2、塑性铰线及其确定
板中连续的一些截面均出现塑性铰,连在一起称为塑性铰线。
板的极限荷载:当板中出现足够数量的塑性铰线后,板成为机动体系,达到其承载能力极限状态而破坏,这时板所承受的荷载为板的极限荷载。
板中塑性铰线的分布形式与以下因素有关:
(1) 板的平面形状
(2) 周边支承条件
(3) 两方向跨中、支座的配筋量
(4) 荷载类型等
3、结构极限承载力分析的基本原理
钢筋混凝土双向板具有一定的塑性性质和塑性变形能力,采用塑性理论进行计算与实际较符合,且可节省钢筋。
双向板为高次超静定结构,按塑性理论求精确解很困难,只能求得上限解和下限解。常用方法有极限平衡法和能量法。
现以极限平衡法为例,进行推导
基本假定
(1) 在最大弯矩处形成塑性铰线
(2) 塑性铰线为直线
(3) 板块视为刚性平面
(4) 最危险塑性铰线,最小极限荷载
(5) 塑性铰线上只作用常量弯矩
计算方法
在实际工程设计中,对于承受均布荷载的矩形板,板的正塑性铰线可采用一种固定的分布形式,即板角部的斜向塑性铰线与板夹角取45°。

2.3.3 双向板肋梁楼盖按塑性理论计算步骤
双向板肋梁楼盖通常是多跨连续,亦即楼盖由一些双向板区格组成。对于内部双向板区格按四边固定单块板计算,边区格及角区格按实际支承情况的单块板计算。掌握了单块双向板的计算方法,也就能计算多跨双向板楼盖。
计算步骤
(1)将楼盖划分为不同的双向板曲格。

2、板的配筋构造
双向板的受力钢筋沿板区格平面纵横两个方向配置,配筋方式有弯起式和分离式两种,与单向板中的配筋方式类似。
(1)按弹性理论计算时:正弯矩钢筋(中间板带,边板带)
负弯矩钢筋(沿支座均匀配置)

(2)按塑性理论计算时:配筋应符合内力计算的假定,跨内正弯矩钢筋可沿全板均匀配置,支座上的负弯矩钢筋按计算值沿支座均匀配置。
双向板受力钢筋的直径、间距和弯起点、切断点的位置,以及沿墙边、墙角处的构造钢筋,均与单向板肋梁楼盖的有关规定相同。