第四节 竖向荷载作用下框架结构内力的近似计算
在竖向荷载作用下,多、高层框架结构的内力可用力法、位移法等结构力学方法计算。工程设计中,如采用手算,可采用迭代法、分层法、弯矩二次分配法及系数法等近似方法计算。
4.4.1 分层法
1、竖向荷载作用下框架结构的受力特点及内力计算假定
(1)不考虑框架结构的侧移对其内力的影响;
(2)每层梁上的荷载仅对本层梁及其上、下柱的内力产生影响,对其他各层梁、柱内力的影响可忽略不计。
应当指出,上述假定中所指的内力不包括柱轴力,因为某层梁上的荷载对下部各层柱的轴力均有较大影响,不能忽略。
2、分层法计算要点
(1)将多层框架沿高度分成若干单层无侧移的敞口框架,每个敞口框架包括本层梁和与之相连的上、下层柱。梁上作用的荷载、各层柱高及梁跨度均与原结构相同。
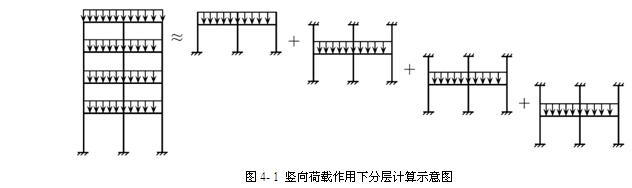
(2)除底层柱的下端外,其他各柱的柱端应为弹性约束。为便于计算,均将其处理为固定端。这样将使柱的弯曲变形有所减小,为消除这种影响,可把除底层柱以外的其他各层柱的线刚度乘以修正系数0.9。
(3)用无侧移框架的计算方法(如弯矩分配法)计算各敞口框架的杆端弯矩,由此所得的梁端弯矩即为其最后的弯矩值;因每一柱属于上、下两层,所以每一柱端的最终弯矩值需将上、下层计算所得的弯矩值相加。在上、下层柱端弯矩值相加后,将引起新的节点不平衡弯矩,如欲进一步修正,可对这些不平衡弯矩再作一次弯矩分配。
如用弯矩分配法计算各敞口框架的杆端弯矩,在计算每个节点周围各杆件的弯矩分配系数时,应采用修正后的柱线刚度计算;并且底层柱和各层梁的传递系数均取1/2,其他各层柱的传递系数改用1/3。
(4)在杆端弯矩求出后,可用静力平衡条件计算梁端剪力及梁跨中弯矩;由逐层叠加柱上的竖向荷载(包括节点集中力、柱自重等)和与之相连的梁端剪力,即得柱的轴力。
4.4.2 弯矩二次分配法
具体计算步骤:
(1)根据各杆件的线刚度计算各节点的杆端弯矩分配系数,并计算竖向荷载作用下各跨梁的固端弯矩。
(2)计算框架各节点的不平衡弯矩,并对所有节点的不平衡弯矩同时进行第一次分配(其间不进行弯矩传递)。
(3)将所有杆端的分配弯矩同时向其远端传递(对于刚接框架,传递系数均取1/2)。
(4)将各节点因传递弯矩而产生的新的不平衡弯矩进行第二次分配,使各节点处于平衡状态。至此,整个弯矩分配和传递过程即告结束。
(5)将各杆端的固端弯矩、分配弯矩和传递弯矩叠加,即得各杆端弯矩。
4.4.3 系数法
系数法是一种更简单的方法,只要给出荷载、框架梁的计算跨度和支承情况,就可很方便地计算出框架梁、柱各控制截面内力。
此法是美国《统一建筑规范》(Uniform Building Code)中介绍的方法,在国际上被广泛采用。
4.4.1 分层法
1、竖向荷载作用下框架结构的受力特点及内力计算假定
(1)不考虑框架结构的侧移对其内力的影响;
(2)每层梁上的荷载仅对本层梁及其上、下柱的内力产生影响,对其他各层梁、柱内力的影响可忽略不计。
应当指出,上述假定中所指的内力不包括柱轴力,因为某层梁上的荷载对下部各层柱的轴力均有较大影响,不能忽略。
2、分层法计算要点
(1)将多层框架沿高度分成若干单层无侧移的敞口框架,每个敞口框架包括本层梁和与之相连的上、下层柱。梁上作用的荷载、各层柱高及梁跨度均与原结构相同。

(2)除底层柱的下端外,其他各柱的柱端应为弹性约束。为便于计算,均将其处理为固定端。这样将使柱的弯曲变形有所减小,为消除这种影响,可把除底层柱以外的其他各层柱的线刚度乘以修正系数0.9。
(3)用无侧移框架的计算方法(如弯矩分配法)计算各敞口框架的杆端弯矩,由此所得的梁端弯矩即为其最后的弯矩值;因每一柱属于上、下两层,所以每一柱端的最终弯矩值需将上、下层计算所得的弯矩值相加。在上、下层柱端弯矩值相加后,将引起新的节点不平衡弯矩,如欲进一步修正,可对这些不平衡弯矩再作一次弯矩分配。
如用弯矩分配法计算各敞口框架的杆端弯矩,在计算每个节点周围各杆件的弯矩分配系数时,应采用修正后的柱线刚度计算;并且底层柱和各层梁的传递系数均取1/2,其他各层柱的传递系数改用1/3。
(4)在杆端弯矩求出后,可用静力平衡条件计算梁端剪力及梁跨中弯矩;由逐层叠加柱上的竖向荷载(包括节点集中力、柱自重等)和与之相连的梁端剪力,即得柱的轴力。
4.4.2 弯矩二次分配法
具体计算步骤:
(1)根据各杆件的线刚度计算各节点的杆端弯矩分配系数,并计算竖向荷载作用下各跨梁的固端弯矩。
(2)计算框架各节点的不平衡弯矩,并对所有节点的不平衡弯矩同时进行第一次分配(其间不进行弯矩传递)。
(3)将所有杆端的分配弯矩同时向其远端传递(对于刚接框架,传递系数均取1/2)。
(4)将各节点因传递弯矩而产生的新的不平衡弯矩进行第二次分配,使各节点处于平衡状态。至此,整个弯矩分配和传递过程即告结束。
(5)将各杆端的固端弯矩、分配弯矩和传递弯矩叠加,即得各杆端弯矩。
4.4.3 系数法
系数法是一种更简单的方法,只要给出荷载、框架梁的计算跨度和支承情况,就可很方便地计算出框架梁、柱各控制截面内力。
此法是美国《统一建筑规范》(Uniform Building Code)中介绍的方法,在国际上被广泛采用。